Flexible and efficient simulation-based inference for models of decision-making
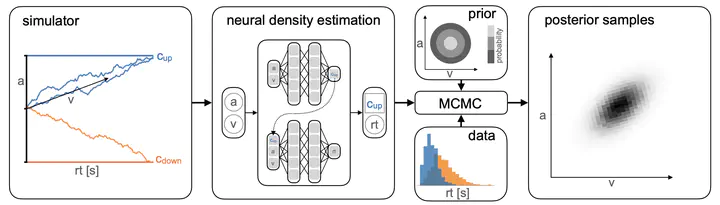 Training a neural likelihood estimator on simulated data to perform parameter inference.
Training a neural likelihood estimator on simulated data to perform parameter inference.
Abstract
Inferring parameters of computational models that capture experimental data is a central task in cognitive neuroscience. Bayesian statistical inference methods usually require the ability to evaluate the likelihood of the model—however, for many models of interest in cognitive neuroscience, the associated likelihoods cannot be computed efficiently. Simulation-based inference (SBI) offers a solution to this problem by only requiring access to simulations produced by the model. Previously, Fengler et al. introduced Likelihood Approximation Networks (LAN, Fengler et al., 2021) which make it possible to apply SBI to models of decision-making, but require billions of simulations for training. Here, we provide a new SBI method that is substantially more simulation-efficient. Our approach, Mixed Neural Likelihood Estimation (MNLE), trains neural density estimators on model simulations to emulate the simulator, and is designed to capture both the continuous (e.g., reaction times) and discrete (choices) data of decision-making models. The likelihoods of the emulator can then be used to perform Bayesian parameter inference on experimental data using standard approximate inference methods like Markov Chain Monte Carlo sampling. We demonstrate MNLE on two variants of the drift-diffusion model (DDM) and show that it is substantially more efficient than LANs. MNLE achieves similar likelihood accuracy with six orders of magnitude fewer training simulations, and is significantly more accurate than LANs when both are trained with the same budget. This enables researchers to perform SBI on custom-tailored models of decision-making, leading to fast iteration of model design for scientific discovery.